欧拉角

 2.4k words

欧拉角是 Leonhard Euler 引入的三个角度，用于描述刚体相对于固定坐标系的方向。

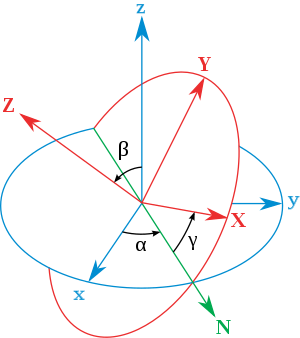
图1 欧拉角的几何定义

固定坐标系(x, y, z)，也成为静态坐标系，世界坐标系，方向轴保持固定不变
旋转坐标系(X, Y, Z)， 刚体自身的坐标系
交点线(N) ，xOy 平面与 XOY 平面的交线

一、几何定义(静态定义)

  • α 或者 (φ) 是 x 轴和 N 轴之间的带符号角度( x 约定，也可以在 y 和 N 之间定义，称之为 y 约定)
  • β 或者 (θ) 是 z 轴和 Z 轴之间的不带符号角度
  • γ 或者 (ψ) 是 N 轴和 X 轴之间的带符号角度( x 约定)

α 角又被称之为进动角，β 角称之为章动角，γ 称之为自旋角。

值域范围

  • α 与 γ 角度范围为 [0, 2π]
  • β 角度范围为 [0, π]

特殊情况：当 β 为 0 或者 π 的时候会出现环架锁定现象。

二、动态定义

动态定义不关注交点线(N)，而是通过描述绕坐标系的不同轴旋转来进行定义。根据选取的坐标系的不同可以区分为内旋(或称固有旋转)(intrinsic rotations) 和外旋 (extrinsic rotations)。

内旋约定

内旋是围绕刚体的XYZ坐标轴进行的基本旋转。因此在每次旋转后坐标轴的朝向都会发生改变。从 XYZ 与 xyz 重合开始，三个固有旋转的组合可以达到 XYZ 的任意方向。

内旋

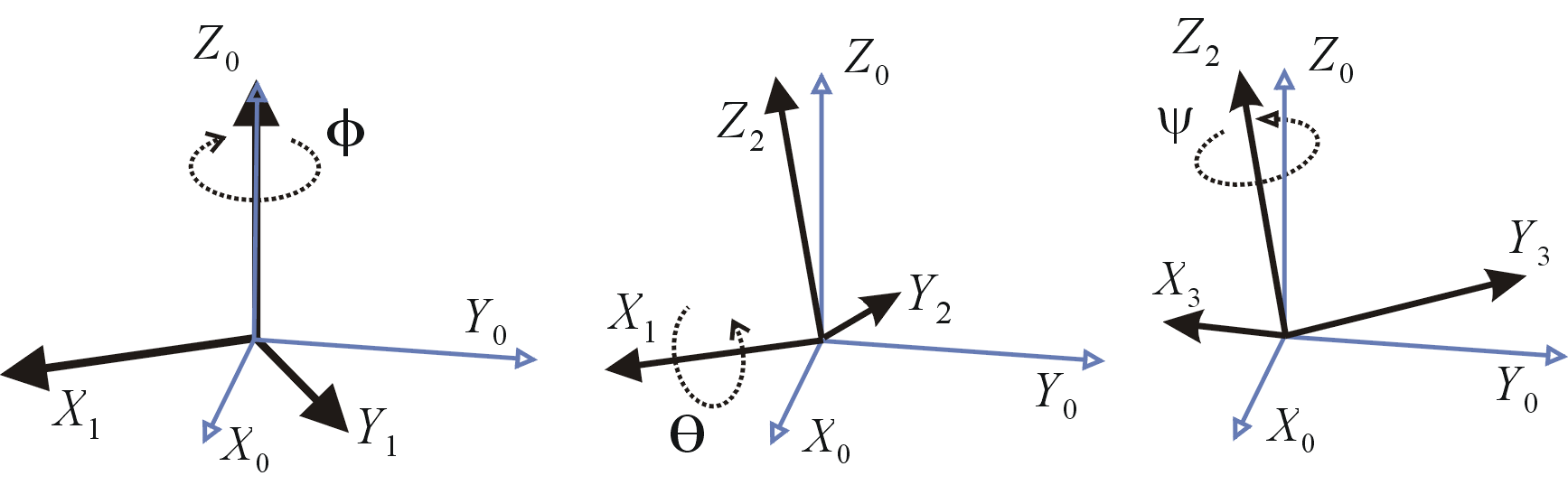
图2 用欧拉角 ( α , β , γ ) = (−60°, 30°, 45°)表示的旋转，使用z-x'-z″内在旋转

比如图2可以通过内旋的方式进行描述。

  1. 物体绕 Z0Z_0 轴旋转 α 角度， 旋转后得到 X1Y1Z0X_1Y_1Z_0
  2. 物体绕 X1X_1 轴旋转 β 角度，旋转后得到 X1Y2Z2X_1Y_2Z_2
  3. 物体绕 Z2Z_2 轴旋转 γ 角度，旋转后得到 X3Y3Z2X_3Y_3Z_2

欧拉角旋转动画

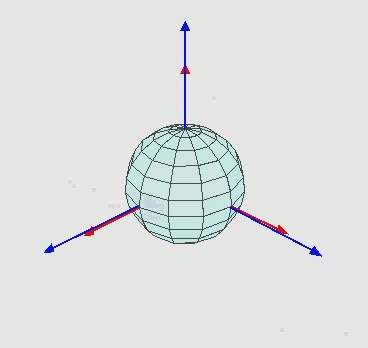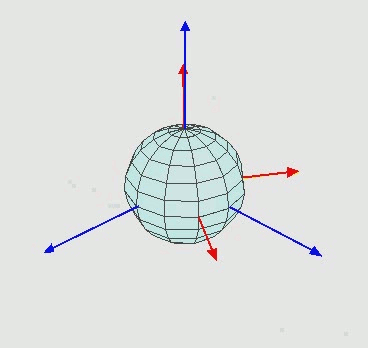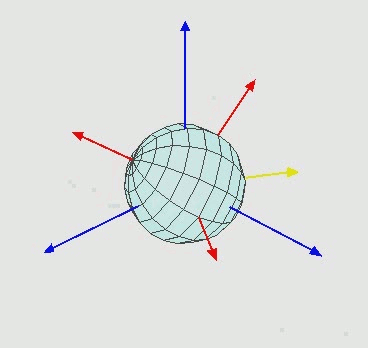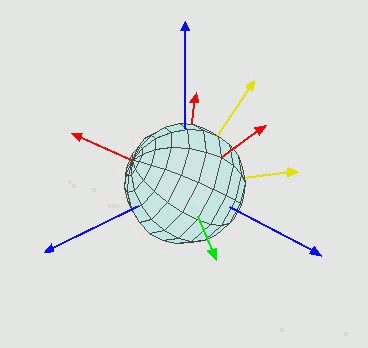
图3 欧拉角旋转动画

旋转矩阵表示内旋

R=Rx(α)∗Ry(β)∗Rz(γ)R = R_x(α) * R_y(β) * R_z(γ)

如果用于左乘列向量，则表示绕轴 X−Y′−Z′′X-Y^{'}-Z^{''} 的内旋组合。

外旋约定

外旋是绕固定轴 xyz 进行的基本旋转。 XYZ 系统旋转，xyz 系统固定。从 XYZ 重叠 xyz 开始，三个外部旋转的组合可以达到 XYZ 的任意方向。

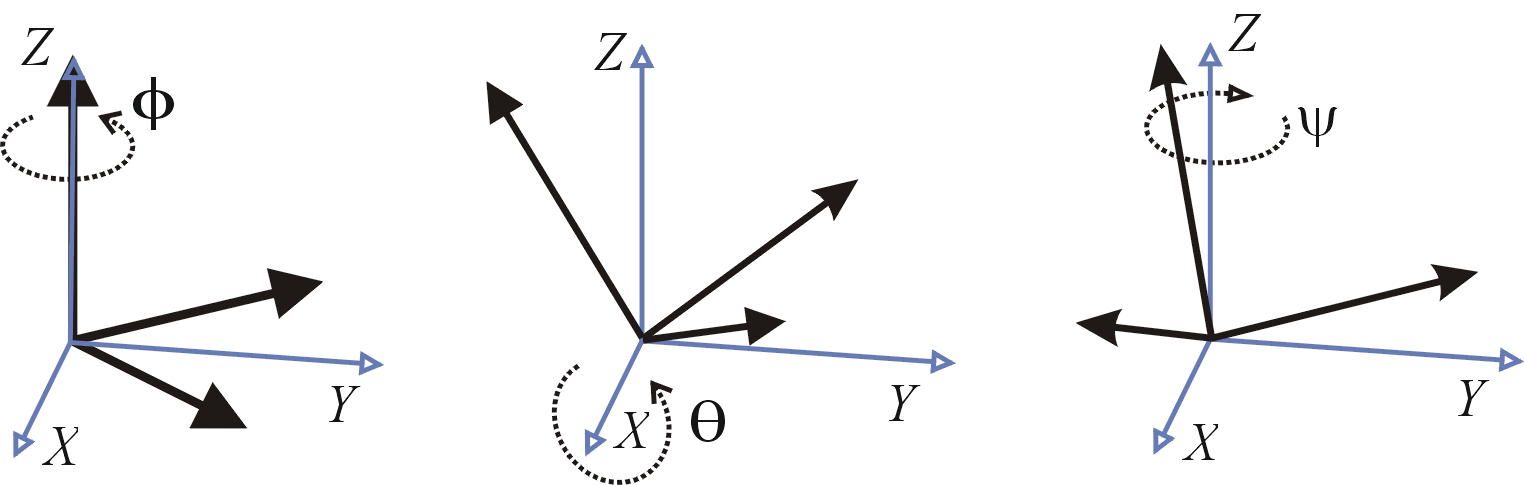
图4 使用zxz外旋转，由 (γ, β, α) = (45°, 30°, -60°) 表示相同的旋转

以图4为例(图中的XYZ其实应为xyz，没有找到更合适的图，就先用这个来表示下)，可以通过下面的旋转方式获取到：

  1. 物体绕 z 轴旋转 γ 角度，X 轴与 x 轴现在成角度 γ
  2. 物体绕 x 轴旋转 β 角度，Z 轴现与 z 轴成角度 β
  3. 物体再次绕 z 轴旋转 α 角度

旋转矩阵表示外旋

R=Rz(γ)∗Ry(β)∗Rx(α)R = R_z(γ) * R_y(β) * R_x(α)

如果用于预乘列向量，则表示绕轴 xyzxyz的外旋组合。

内旋与外旋的转换

任何的外旋都等于角度相同但元素旋转顺序相反的内旋，反之亦然。例如：角度α、β、γ的内旋 X−Y′−Z′′X-Y^{'}-Z^{''}相当于角度γ、β、α的外旋zyxzyx。两者都可用矩阵 R=Rx(α)∗Ry(β)∗Rz(γ)R = R_x(α) * R_y(β) * R_z(γ)表示。
证明过程可以参考

三、描述方式

欧拉角可以通过通过基本几何或者基本旋转(内旋，或者外旋)的组合来定义。
在不考虑使用两种不同的约定来定义旋转(内旋或外旋)的可能性下，存在12种可能得旋转轴序列，分为两组：

Proper Euler angles

也称为真欧拉角或者经典欧拉角。经典欧拉角中第一旋转轴和第三旋转轴是相同的，共有6种可能序列：

  • z1−x′−z2′′z_1-x^{'}-z_2^{''} (内旋) 或 z2−x−z1z_2-x-z_1 (外旋)
  • z1−y′−z2′′z_1-y^{'}-z_2^{''} (内旋) 或 z2−y−z1z_2-y-z_1 (外旋)
  • x1−y′−x2′′x_1-y^{'}-x_2^{''} (内旋) 或 x2−y−x1x_2-y-x_1 (外旋)
  • x1−z′−x2′′x_1-z^{'}-x_2^{''} (内旋) 或 x2−z−x1x_2-z-x_1 (外旋)
  • y1−x′−y2′′y_1-x^{'}-y_2^{''} (内旋) 或 y2−x−y1y_2-x-y_1 (外旋)
  • y1−z′−y2′′y_1-z^{'}-y_2^{''} (内旋) 或 y2−z−y1y_2-z-y_1 (外旋)

Tait–Bryan angles

也称为泰特-布莱恩角，万向角，航海角度，或者直接描述三个角(航向，海拔和高度或者偏航，俯仰和滚动) 。泰特-布莱恩角中三个角分别绕三个不同的轴转动，共有6种可能得序列：

  • x−y′−z′′x-y^{'}-z^{''} (内旋) 或 z−y−xz-y-x (外旋)
  • x−z′−y′′x-z^{'}-y^{''} (内旋) 或 y−z−xy-z-x (外旋)
  • y−x′−z′′y-x^{'}-z^{''} (内旋) 或 z−x−yz-x-y (外旋)
  • y−z′−x′′y-z^{'}-x^{''} (内旋) 或 x−z−yx-z-y (外旋)
  • z−x′−y′′z-x^{'}-y^{''} (内旋) 或 y−x−zy-x-z (外旋)
  • z−y′−x′′z-y^{'}-x^{''} (内旋) 或 x−y−zx-y-z (外旋) 内旋称之为：偏航，俯仰和滚动

上面12组为合法的欧拉角组，唯一的限制是任何两个相邻的旋转，必须围绕不同的转动轴旋转。
经典力学常用 zxz 顺规来设定，按第二个转动轴名，又简称之为 x顺规。量子力学、核子物理学、粒子物理学常用 y顺规来描述。而在航空航天工程学中常用 xyz顺规(Tait-Bryan 角)。

四、其他表达方式

旋转矩阵

任何方向都可以从初始方向开始组合三个基本旋转来实现。等价的，任何旋转矩阵 R 都可以分解为三个基本旋转矩阵的乘积。例如：

R=Rx(α)∗Ry(β)∗Rz(γ)R = R_x(α) * R_y(β) * R_z(γ)

是一个旋转矩阵，可以用于表示围绕轴 zyxzyx(按顺序) 的外旋的组合，或者围绕 X−Y′−Z′′X-Y^{'}-Z^{''}(按顺序) 的内旋组合。
内旋右乘，外旋左乘。

详细的内容可以参考变换矩阵与坐标系变换中旋转矩阵部分

在应用旋转矩阵时需要确认3个点：

  1. 旋转顺序
  2. 内旋还是外旋
  3. 三个旋转角度

有这三个点的信息，便可以获知如何应用旋转矩阵。

四元数

四元数的定义及其性质，以下部分关注于欧拉角与四元数的转化。

直接给出转化公式

泰特-布莱恩角
XYZ this.x=s1∗c2∗c3+c1∗s2∗s3;this.y=c1∗s2∗c3−s1∗c2∗s3this.z=c1∗c2∗s3+s1∗s2∗c3;this.w=c1∗c2∗c3−s1∗s2∗s3;this.x = s1 * c2 * c3 + c1 * s2 * s3; \\ this.y = c1 * s2 * c3 - s1 * c2 * s3 \\this.z = c1 * c2 * s3 + s1 * s2 * c3; \\this.w = c1 * c2 * c3 - s1 * s2 * s3;
YXZ this.x=s1∗c2∗c3+c1∗s2∗s3;this.y=c1∗s2∗c3−s1∗c2∗s3;this.z=c1∗c2∗s3−s1∗s2∗c3;this.w=c1∗c2∗c3+s1∗s2∗s3;this.x = s1 * c2 * c3 + c1 * s2 * s3;\\this.y = c1 * s2 * c3 - s1 * c2 * s3;\\this.z = c1 * c2 * s3 - s1 * s2 * c3;\\this.w = c1 * c2 * c3 + s1 * s2 * s3;
ZXY this.x=s1∗c2∗c3−c1∗s2∗s3;this.y=c1∗s2∗c3+s1∗c2∗s3;this.z=c1∗c2∗s3+s1∗s2∗c3;this.w=c1∗c2∗c3−s1∗s2∗s3;this.x = s1 * c2 * c3 - c1 * s2 * s3;\\this.y = c1 * s2 * c3 + s1 * c2 * s3;\\this.z = c1 * c2 * s3 + s1 * s2 * c3;\\this.w = c1 * c2 * c3 - s1 * s2 * s3;
ZYX this.x=s1∗c2∗c3−c1∗s2∗s3;this.y=c1∗s2∗c3+s1∗c2∗s3;this.z=c1∗c2∗s3−s1∗s2∗c3;this.w=c1∗c2∗c3+s1∗s2∗s3;this.x = s1 * c2 * c3 - c1 * s2 * s3;\\this.y = c1 * s2 * c3 + s1 * c2 * s3;\\this.z = c1 * c2 * s3 - s1 * s2 * c3;\\this.w = c1 * c2 * c3 + s1 * s2 * s3;
YZX this.x=s1∗c2∗c3+c1∗s2∗s3;this.y=c1∗s2∗c3+s1∗c2∗s3;this.z=c1∗c2∗s3−s1∗s2∗c3;this.w=c1∗c2∗c3−s1∗s2∗s3;this.x = s1 * c2 * c3 + c1 * s2 * s3;\\this.y = c1 * s2 * c3 + s1 * c2 * s3;\\this.z = c1 * c2 * s3 - s1 * s2 * c3;\\this.w = c1 * c2 * c3 - s1 * s2 * s3;
XZY this.x=s1∗c2∗c3−c1∗s2∗s3;this.y=c1∗s2∗c3−s1∗c2∗s3;this.z=c1∗c2∗s3+s1∗s2∗c3;this.w=c1∗c2∗c3+s1∗s2∗s3;this.x = s1 * c2 * c3 - c1 * s2 * s3;\\this.y = c1 * s2 * c3 - s1 * c2 * s3;\\this.z = c1 * c2 * s3 + s1 * s2 * c3;\\this.w = c1 * c2 * c3 + s1 * s2 * s3;

五、旋转的意义

数学意义：数学中的旋转常指主动旋转，例如向量的旋转
物理意义：物理学和工程中旋转可以为主动旋转，也可以为被动旋转，例如slam坐标系旋转

参考文档

Tags: ,