变换矩阵

最近的工作又涉及到了 3D 空间内的坐标系变换。虽然之前也有接触过相关的工作内容，但都只了解了其中的一部分。这次从头开始进行开发便有点捉襟见肘了。没得办法，从头开始学习下变换矩阵相关的内容了。本文将从简单的 2D 变换矩阵开始，扩展到 3D 变换矩阵。最后再应用变换矩阵进行坐标系变换。

变换矩阵(Transformation matrix)的定义可以从维基百科中查找到，这里就不在赘言。本篇文章会涉及到向量、矩阵等知识的内容。关于向量和矩阵的定义、性质以及计算等信息不在本文中描述。如有需要可自行查阅相关知识后再阅读后续内容。

在开始之前，需要先同步以下约定信息：

1. 向量统一为列向量，即 $\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}$ 或者写为行向量的转置 $\begin{bmatrix} x & y & z \end{bmatrix} ^\mathsf{T}$

2. 原向量左乘变换矩阵得到目标向量，即 $\begin{bmatrix} X & Y & Z \end{bmatrix} ^\mathsf{T} = M * \begin{bmatrix} x & y & z \end{bmatrix} ^\mathsf{T}$

3. 因使用列向量来表示，下文中的矩阵乘法除额外指出外均为左乘

一、2D 变换矩阵

缩放

缩放和旋转，需要留意的一点是都是基于原点的操作。以缩放为例，可以理解为将图形的左下角钉在原点，然后拉扯图形的右上角，造成图形的均匀形变。

缩放和旋转的这个性质也可以称为线性变换。

均匀缩放

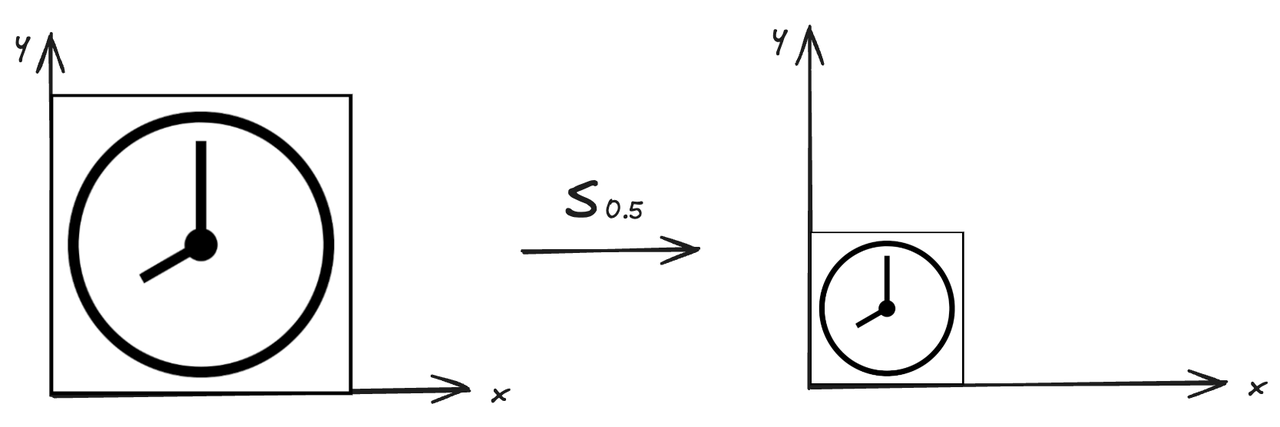
图1 x,y缩放为原来的0.5

右侧的图形的 x 值和 y 值都缩放为原来的 1/2 。
可以很简单的写出缩放公式为：$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} s & 0 \\ 0 & s \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix}$

非均匀缩放

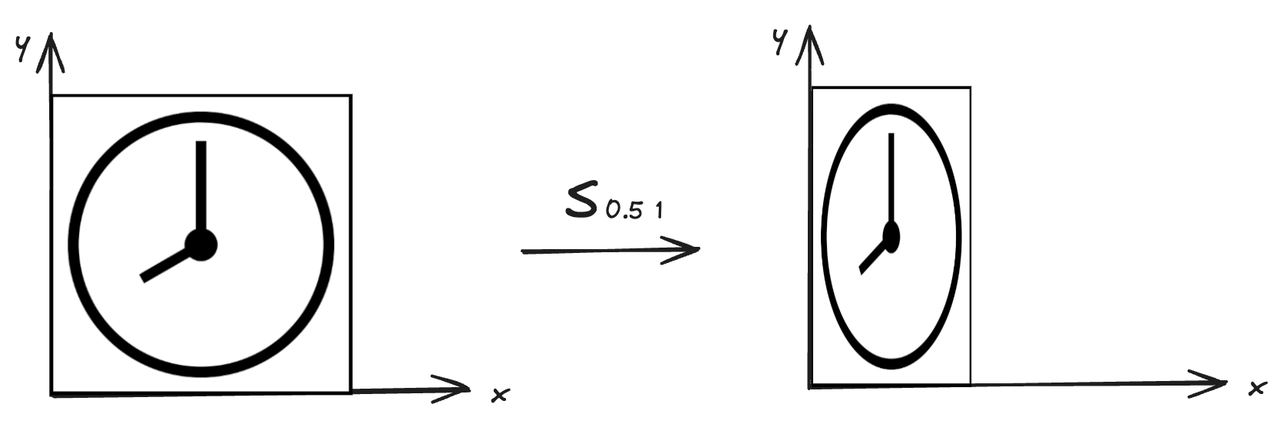
图2 y不变，x缩放为原来的0.5

如果只有一个轴向的缩放，另一个轴向保持不变，比如上图的 x 值变为原来的 1/2， y 值保持不变。
此时的缩放公式为：$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix}$ ，在上方的案例中，$s_x = 0.5$ ,$s_y = 1$

切变

图3 切变

以水平切变为例。我们把图形想象成具有弹性，把下边固定，上边沿着 x 轴移动 a 距离后，得到水平切变后的图形。
分析切变前后的横纵坐标变化可以得到：

$x^\mathsf{'} = x + a * y \\ y^\mathsf{'} = y$

由此得出案例的缩放公式为：

$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix}$

旋转

图4 旋转45°

说到旋转那就得要确定好旋转中心和旋转正方向。如果没有特殊声明的情况下，默认旋转的中心点是原点，旋转的正方向是逆时针方向。比如上图可以描述为图形旋转45°。

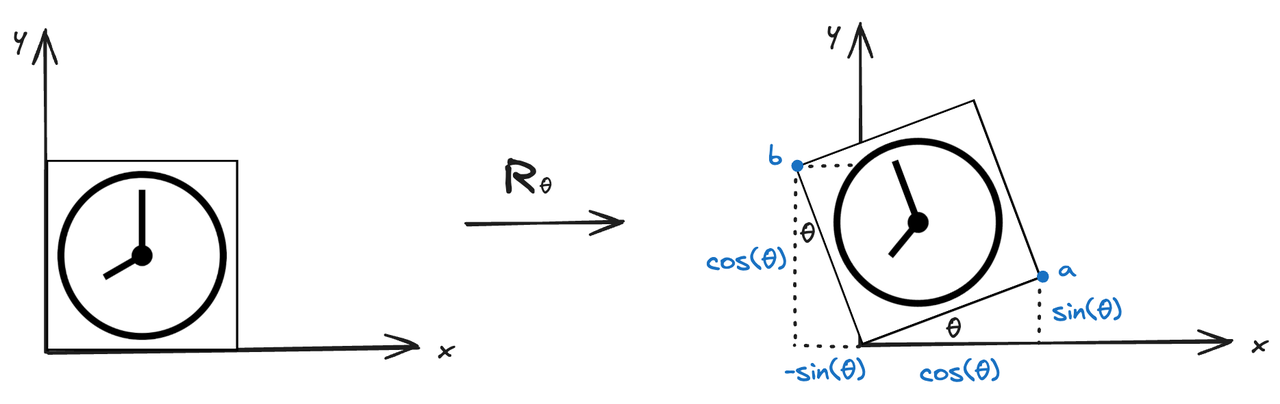
图5 旋转

以上图旋转 θ 角度为例:

a 点旋转前的坐标为$\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ 旋转后的坐标为$\begin{bmatrix} cos(θ) \\ sin(θ) \end{bmatrix}$

b点旋转前的坐标为$\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ 旋转后的坐标为$\begin{bmatrix} -sin(θ) \\ cos(θ) \end{bmatrix}$

将旋转前后的 a，b 点坐标带入公式$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} m_{11} & m_{12} \\ m_{11} & m_{22} \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix}$后可以得到，旋转矩阵为

$R(θ) = \begin{bmatrix} cos(θ) & -sin(θ) \\ sin(θ) & cos(θ) \\ \end{bmatrix}$

线性变换

观察缩放矩阵和旋转矩阵，它们都可以写成类似下式的形式：

$x^\mathsf{'} = a*x + b*y \\ y^\mathsf{'} = c*x + d*y$

采用矩阵的形式便是：

$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix}$

类似这种形式，我们将之称为线性变换。

平移、仿射变换与齐次坐标

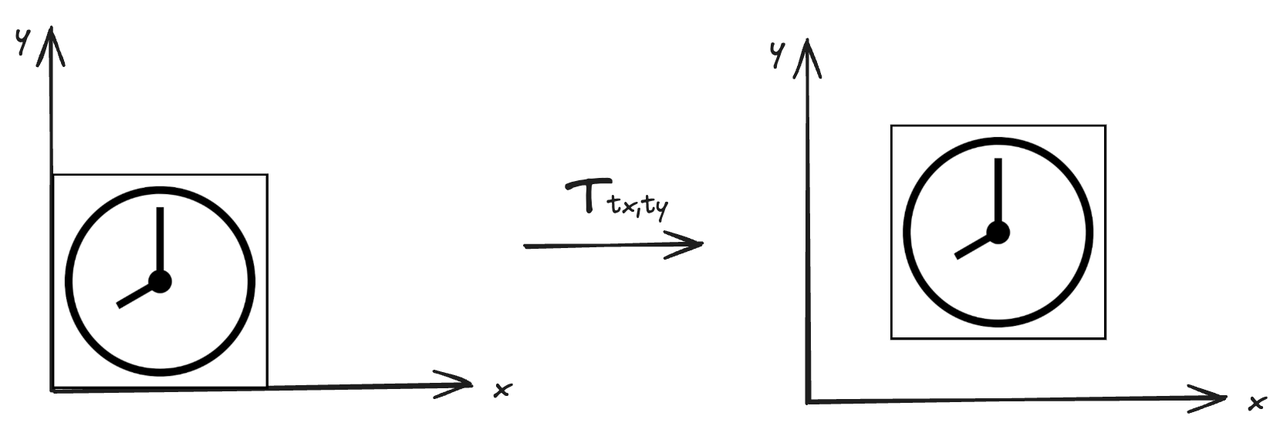
图6 平移

缩放变换和旋转变换都是线性变换。但还有一种与他们不同的变换 - 平移变换，他的不同之处在于是非线性的(也被称为仿射变换)。

以上图的平移变换为例，左边图形的x 坐标平移 tx，y 坐标平移 ty 得到右侧的图形。

我们可以很简单的写出坐标的变换公式，如下：

$x^\mathsf{'} = x + t_x \\ y^\mathsf{'} = y + t_y$

观察上述的公式，我们似乎不能简单的写为：

$X^\mathsf{'} = M * X$

而是要在此基础上添加一个常量部分：

$X^\mathsf{'} = M * X + b$

写为矩阵的形式便是：

$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \\ \end{bmatrix}$

我们并不希望将平移变换当成一个特殊的变换，处理的方式和缩放变换、旋转变换不同。那有没有方式可以将平移变换与缩放变换、旋转变换统一起来，都是 $X^\mathsf{'} = M * X$ 的形式呢？
答案是有的，那便是引入齐次坐标。

齐次坐标

齐次坐标是在原来2维坐标的基础上添加一个维度

• 2D 点变为 $\begin{bmatrix} x & y & 1 \end{bmatrix} ^\mathsf{T}$

• 2D 向量变为 $\begin{bmatrix} x & y & 0 \end{bmatrix} ^\mathsf{T}$

引入齐次坐标后，上述的平移矩阵变可以写为如下的形式：

$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ w^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \\ \end{bmatrix}$

简单的解释下为什么点添加的值为 1，而向量添加的值为 0。
以 x 坐标的计算为例，一个点在经过平移变换时，计算为 :

$x^\mathsf{'} = 1 * x + 0 * y + 1 * t_x$

可以看到添加的值 1 的作用便是应用 $t_x$的平移变化。
而向量是指向的方向，对一个向量应用平移变化，得到的应该还是向量本身。所以向量添加的齐次坐标为 0。

仿射变换

形如 $\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \\ \end{bmatrix}$的形式，我们将之称为仿射变换。仿射变换与齐次坐标下的形式是等价的。

变换矩阵

引入齐次坐标后，上述的三个变换可以改写为齐次坐标的形式

缩放矩阵

$S(s_x, s_y) = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}$

旋转矩阵

$R(θ) = \begin{bmatrix} cos(θ) & -sin(θ) & 0 \\ sin(θ) & cos(θ) & 0 \\ 0 & 0 & 1 \end{bmatrix}$

平移矩阵

$T(t_x, t_y) = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}$

逆变换

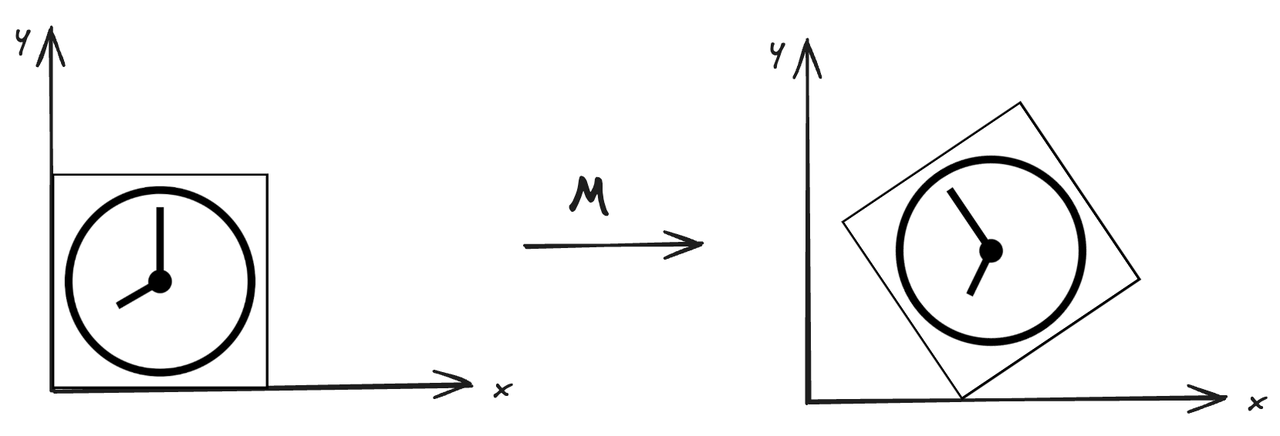
图7 变换

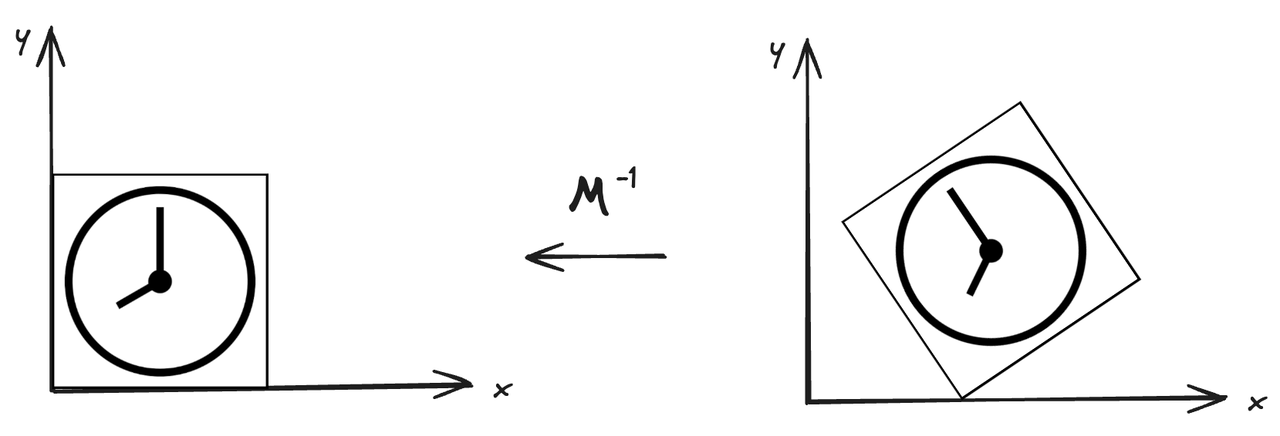
图8 逆变换

假设一个图像如图7左侧一样经历了一系列变换得到图7右侧的形状。所经历的变换为：

$X^\mathsf{'} = M * X$

那想要将形状还原为原来的形状，如图8一样，那所经历的变换便是图7变换的逆变换：

$X = M^\mathsf{-1} * X^\mathsf{'}$

其中 $M^\mathsf{-1}$为变换 $M$的逆矩阵。

旋转矩阵性质

以2维旋转矩阵为例：

$R(θ) = \begin{bmatrix} cos(θ) & -sin(θ) \\ sin(θ) & cos(θ) \\ \end{bmatrix} \\$ $R(-θ) = \begin{bmatrix} cos(θ) & sin(θ) \\ -sin(θ) & cos(θ) \\ \end{bmatrix} = R(θ)^\mathsf{T}$

而 $R(-θ) = R(θ)^\mathsf{-1}$

所以得到 $R(-θ) = R(θ)^\mathsf{T} = R(θ)^\mathsf{-1}$

缩放、旋转与平移的顺序

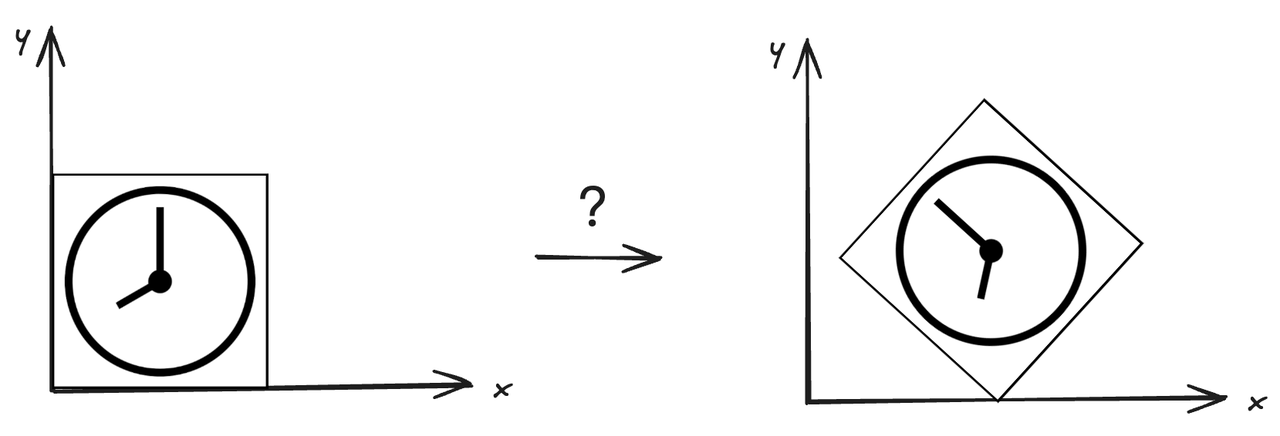
图9 如何变换

面对如图9的变换是怎么得到的呢？对于一个复杂的变换，我们可以将其进行拆解，拆解为基础的缩放变换、旋转变换和平移变换，并对这些基础的变换进行组合。从图9中我可以看出包含旋转变换和平移变换，那是要先进行平移变换还是先进行旋转变换呢？我们接下来分别进行尝试。

先平移变换后旋转变换

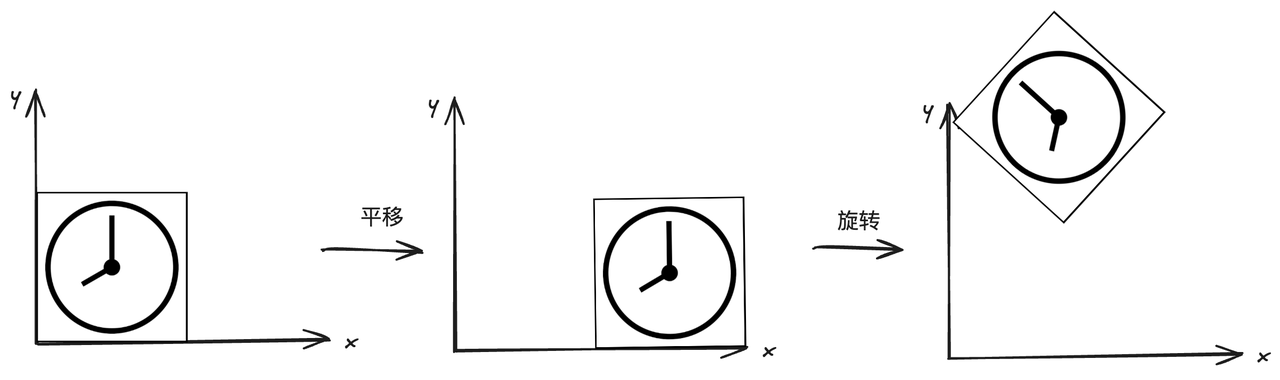
图10 先平移后旋转

我们可以先对原图形进行平移变换得到图10的中间图形，然后在对其进行旋转变换。在进行旋转变换的时候需要留意一点，旋转是基于旋转中心(原点)的操作，在旋转后发现图形不是我们想要的结果。

先旋转变换后平移变换

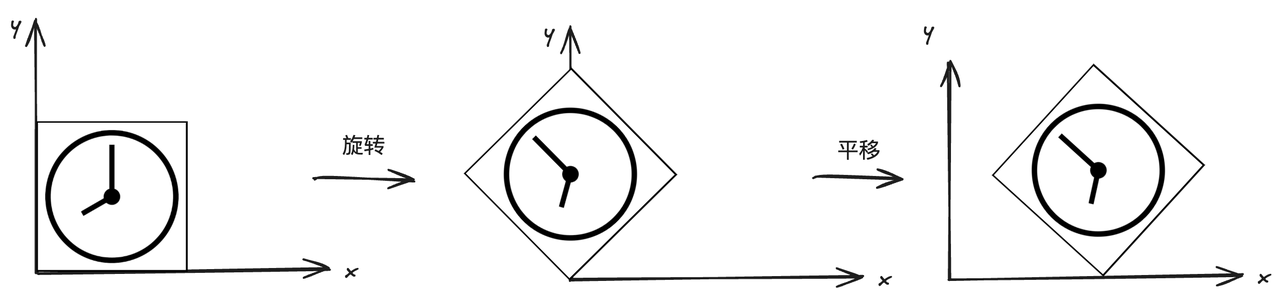
图11 先旋转后平移

那我们先对图形进行旋转变换得到图11的中间图形，然后对其进行平移变换，得到了目标图形。
我们可以从矩阵的角度来理解这个问题
图10的操作可以简写为：

$X^\mathsf{'} = R(θ) * T(t_x,t_y) * X$

图11的操作可以简写为：

$X^\mathsf{'} = T(t_x,t_y) * R(θ) * X$

而矩阵是不满足乘法的交换律，也即：

$R(θ) * T(t_x,t_y) ≠ T(t_x,t_y) * R(θ)$

由此可见缩放、旋转和平移变换的顺序十分重要，一般应用的过程中会按先缩放，后旋转，最后平移的方式来进行组合。

变换的合成与分解

$A_n (... A_2 (A_1 (X))) = An * ... * A2 * A1 * \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}$

对于坐标 $X$ 应用变换$A_1$后应用变换$A_2$ … 一直应用到变换 $A_n$， 可以将

$An * ... * A2 * A1$ 合成得到变换 $M$，之后便可对每个坐标应用变换 $M$，这个性质在进行3D渲染时十分有用。

在图11的过程中，我们应用到了变换的分解，将一个复杂的变换分解成简单的变换。

主动变换和被动变换

主动变换

Active or ablibi trnasformations。坐标系基底不变，物体进行缩放、旋转和平移等操作，矩阵左乘。

被动变换

Passive or alias trnasformations。物体不动，坐标系发生缩放、旋转平移等操作，矩阵右乘。

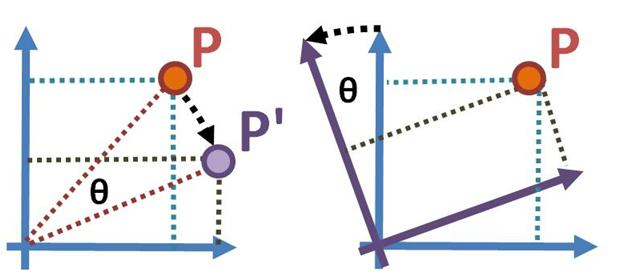图12 主动变换和被动变换

在主动变换（上图左）中，点P通过绕固定坐标系原点顺时针旋转角度θ变换为点P ‘ 。在被动变换（上图右）中，点P保持固定，而坐标系绕其原点逆时针旋转角度θ。主动变换后P ‘相对于原始坐标系的坐标与P相对于旋转坐标系的坐标相同。

主动变换和被动变换互为逆过程。

二、3D 变换矩阵

上面我们详细的讲解了2维的变换，对于3维变换可以类比来进行推导。

齐次坐标

• 3D 点变为 $\begin{bmatrix} x & y & z & 1 \end{bmatrix} ^\mathsf{T}$

• 3D 向量变为 $\begin{bmatrix} x & y & z & 0 \end{bmatrix} ^\mathsf{T}$

三维的变换矩阵为以下的形式：

$\begin{bmatrix} x^\mathsf{'} \\ y^\mathsf{'} \\ z^\mathsf{'} \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}$

缩放矩阵

$S(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 1 & 1 \end{bmatrix}$

旋转矩阵

分别绕z、y、z轴的旋转矩阵如下：

$R_x(α) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos(α) & -sin(α) & 0 \\ 0 & sin(α) & cos(α) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

$R_y(β) = \begin{bmatrix} cos(β) & 0 & sin(β) & 0 \\ 0 & 1 & 0 & 0 \\ -sin(β) & 0 & cos(β) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

$R_z(γ) = \begin{bmatrix} cos(γ) & -sin(γ)& 0 & 0 \\ sin(γ) & cos(γ) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

将其进行组合后的旋转矩阵为(绕自身轴转动的主动旋转，使用右乘表达)：

$R(α, β, γ) = R_x(α) * R_y(β) * R_z(γ)$

注意针对欧拉角的不同约定会有不同的描述形式，上述的描述xyz顺规的泰特-布莱恩角形式。其中绕 x 轴转动称为 roll，绕 y 轴转动称为 pitch，绕 z 轴转动称为 yaw。

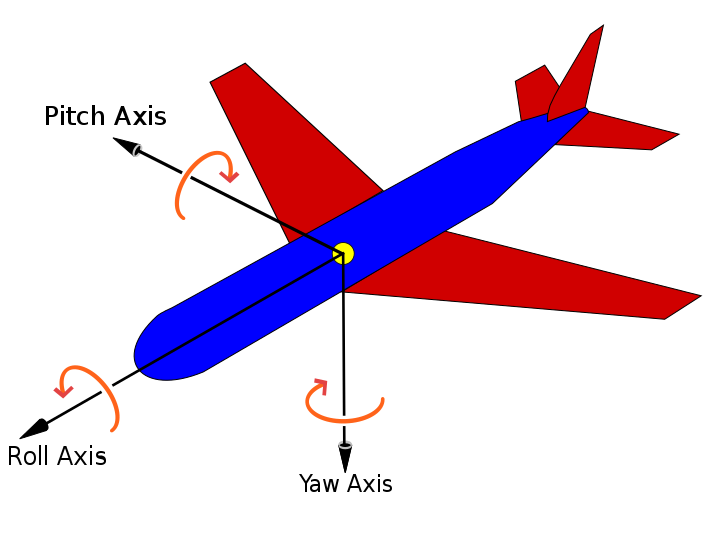图13 xyz顺归的泰特-布莱恩角

旋转方向

左手坐标系采用左手螺旋定则来确定正方向，右手坐标系采用右手螺旋定则来确定正方向。

平移矩阵

$T(t_x, t_y, t_z) = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$

变换矩阵

$M = T(t_x, t_y, t_z) * R(α, β, γ) *S(s_x, s_y, s_z)$

代表先进行缩放变换，再进行旋转变换，最后进行平移变换。

三、坐标系变换

接下来分别在 2D 空间和 3D 空间演示下如何求解变换矩阵。

2D 坐标系变换

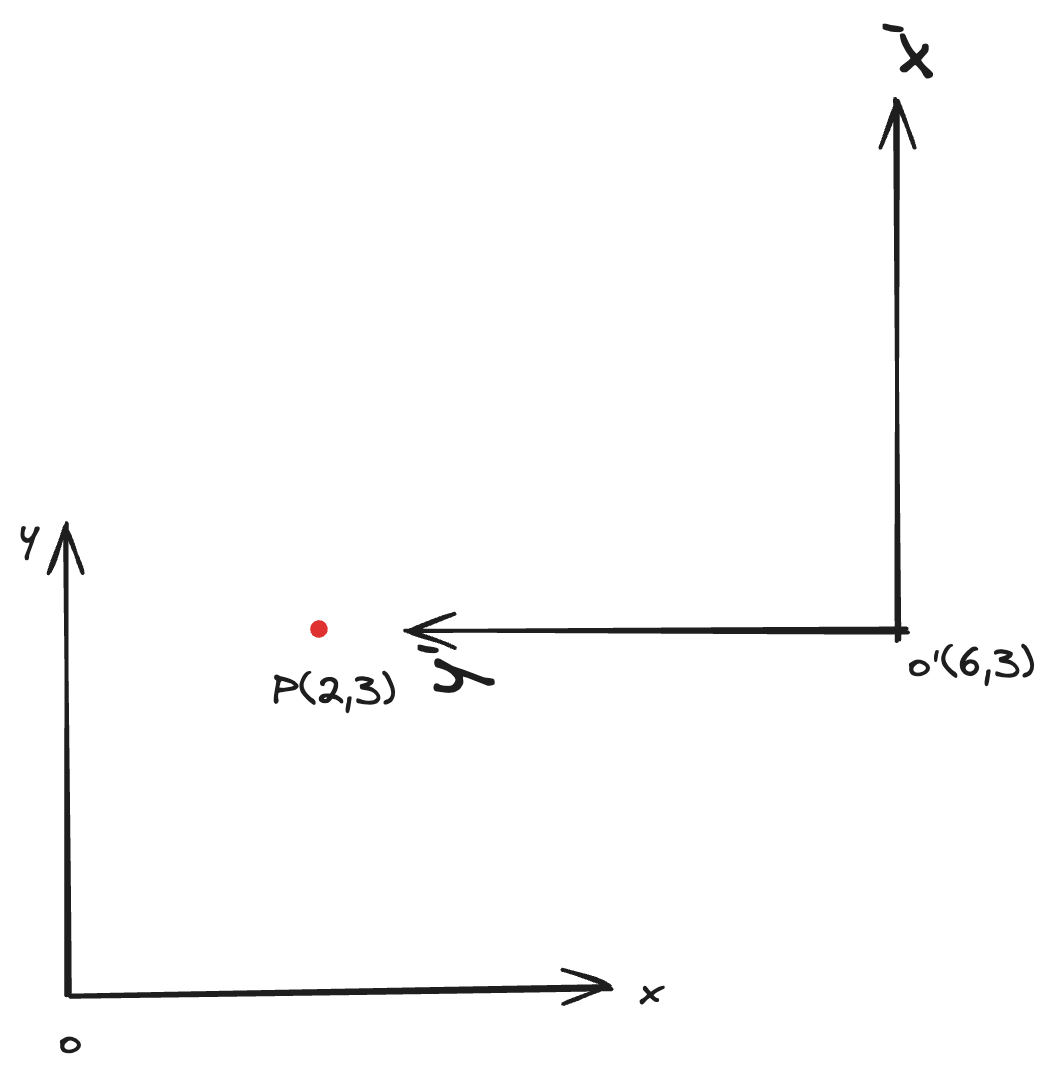图14 2D坐标系转换示例

如图14所示，原有坐标系 $A_{xoy}$以及坐标系内的一点 $P(2,3)$,现需要求出$P(2,3)$在 $B_{x'o'y'}$坐标系中的坐标$P^{'}(x^{'},y^{'})$，计算公式如下：

$P^{'} = M_{A->B} * P$

求解变换矩阵$M_{A->B}$的过程，其实是描述如何由 $B_{x'o'y'}$坐标系变换到 $A_{xoy}$坐标系的过程(这里描述的是主动变换的过程，而 $A_{xoy}$ 坐标系变换到$B_{x'o'y'}$ 坐标系是被动变换，两者之间互为逆过程)。

1. 坐标系 $B_{x'o'y'}$ 进行平移变换 $T(-6,-3)$ 得到 $B^{'}_{x'oy'}$

2. 坐标系$B^{'}_{x'oy'}$ 旋转 -90° 得到 $A_{xoy}$

$P^{'} = R(-90) * T(-6,-3) * P$

得到

$M_{A->B} = \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & -6 \\ 0 & 1 & -3 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & -3 \\ -1 & 0 & 6 \\ 0 & 0 & 1 \end{bmatrix}$

带入$P^{'} = M_{A->B} * P$可得

$P^{'} = \begin{bmatrix} 0 & 1 & -3 \\ -1 & 0 & 6 \\ 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 4 \\ 1 \end{bmatrix}$

由原图观察可得 $P^{'}(x^{'},y^{'})$ 坐标确实为$\begin{bmatrix} 0 \\ 4 \end{bmatrix}$

PS: $P^{'} = R(-90) * T(-6,-3) * P$ 为主动变换的描述，采用被动变换的描述可以等价为 $P^{'} = (T(6,3) * R(90))^{-1} * P \\ = R(90)^{-1} * T(6,3)^{-1} * P \\ = R(-90) * T(-6,-3) * P$

3D 坐标系变换

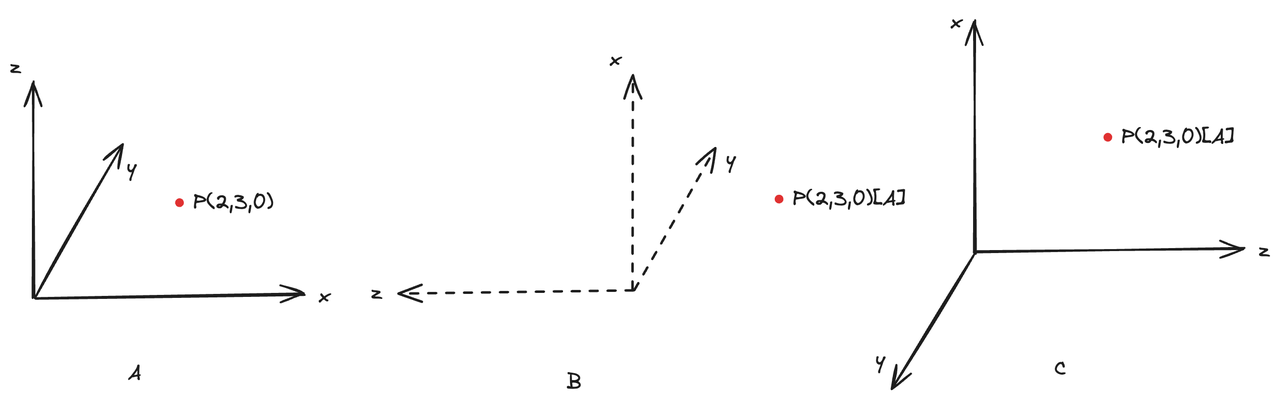
图15 3D坐标系转换示例

如图15所示，原有坐标系 $A_{xyz}$以及坐标系内的一点 $P(2,3,0)$,现需要求出$P(2,3,0)$在 $C_{xyz}$坐标系中的坐标$P^{'}(x^{'},y^{'},z^{'})$，计算公式如下：

$P^{'} = M_{A->C} * P$

求解变换矩阵$M_{A->C}$的过程，其实是描述如何由 $C_{xyz}$坐标系变换到 $A_{xyz}$坐标系的过程主动变换描述）。
观察坐标系的变化，发现只有旋转变换，所以计算公式变为：

$P^{'} = R_{C->A} * T(0,0,0) * P = R_{C->A} * P$

接下来看如何计算旋转矩阵。
直接找到坐标系$C_{xyz}$ 到坐标系$A_{xyz}$的旋转变化有点困难，我们可以加一个中间坐标系$B_{xyz}$。
计算旋转矩阵按旋转参考系的不同可以分为内旋(绕自身轴)和外旋(绕固定轴)，分别进行计算如下：

绕自身轴

由观察可知：

1. 坐标系$C_{xyz}$绕自身 x 轴旋转 180°得到坐标系$B_{xyz}$

2. 坐标系$B_{xyz}$绕自身 y 轴转动 90° 得到坐标系 $C_{xyz}$

3. 两次旋转右乘得到旋转矩阵

$R_{C->A} = R_x(180) * R_y(90) \\$
$= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos(α) & -sin(α) & 0 \\ 0 & sin(α) & cos(α) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} cos(β) & 0 & sin(β) & 0 \\ 0 & 1 & 0 & 0 \\ -sin(β) & 0 & cos(β) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\$
$= \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

绕固定轴：

由观察可知：

1. 坐标系$C_{xyz}$绕固定轴 x 旋转 180° 得到坐标系$B_{xyz}$

2. 坐标系$B_{xyz}$绕固定轴 y 转动 -90° 得到坐标系 $A_{xyz}$

3. 两次旋转左乘得到旋转矩阵

$R_{C->A} = R_y(-90) * R_x(180) \\$
$= \begin{bmatrix} cos(β) & 0 & sin(β) & 0 \\ 0 & 1 & 0 & 0 \\ -sin(β) & 0 & cos(β) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos(α) & -sin(α) & 0 \\ 0 & sin(α) & cos(α) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\$
$= \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

可以看到两种计算方式得到的旋转矩阵是相同的。带入到公式 $P^{'} = R_{A->C} * P$ 中，得到 $P^{'}$坐标为$\begin{bmatrix} 0 \\ -3 \\ 2 \end{bmatrix}$。